Matematická kouzla


Úkoly

Výsledky:

  1. viz. obr1
    obr1
  2. letec může startovat z kteréhokoli místa na rovnoběžce, která má tu vlastnost, že leží 100 km na sever od rovnoběžky, která se nachází blízko jižního pólu a je právě 100 km dlouhá. Viz obr.2
    obr2
  3. Navineme těsně na nějakou tyčku, hřebík nebo tužku. Jestliže např. navineme 20 závitů měří 6 mm, průměr drátu vypočteme dělením ččísla 6 číslem 20.
  4. Uvažujeme takto: Jestliže by nezůstala ani jedna ovce v dvojřadu, trojřadu, čtyřřadu, pětiřadu a šestiřadu, šlo by o společný násobek těchto čísel. Tudíž n (2, 3, 4, 5, 6) = 60
    další násobky jsou: 60, 120, 180, 240, 300, ... .
    Hledejme mezi čísly 61, 121, 181, 241, 301, ... . číslo dělitelné sedmi.
    Naší úloze vyhovuje číslo 301.
  5. Jedno z řešení je např. toto: Z 8litrové nádoby naplníme 5litrovou nádobu. V 8litroé zůstanou 3 litry. Z 5litrové odlijeme 3 litry do 3litrové nádoby, takže v 5litrové zůstanou 2 litry. 3 litry z 3litrove nádoby přelijeme do první nádoby, v níž takto bude 6 litrů vody. Vodu z druhé nádoby přelijeme do třetí nádoby.Z první přelijeme do druhé 5 litrů, takže v první zůstane 1 litr. Z druhé přelijeme do třetí 1 littr a z třetí přelijeme do první všechnu vodu. V první a v druhé nádobě budeme mít po čtyřech litrech.
  6. Označme myšlené číslo písmenem x. Podíly, které vzniknou dělením čísla x čísly 3, 4, 5, označme písmeny a,b,c a zbytka písmeny r1, r2, r3.
    Platí vztahy: 
              x = 3a + r1,
          x = 4b + r2,
          x = 5c + r3.

    Z toho r1 = x - 3a, r2 = x - 4b, r3 = x - 5c.
    Dosadíme:
    S = 40r1 + 45r2 + 36r3 = 121x - 120a - 180b - 180c.
    Činitele 40, 45, 36 jsme vybrali tak, aby všichni sčítanci algebraického součtu byli beze zbytku dělitelní60, kromě 121x. Pokud tento člen dělíme 60, dostaneme zbytek, který se rovná myšlenému číslu x.
    Příklad: Nechť je myšlené číslo 14. První zbytek jsou 2, druhý též 2 a třetí 4. (r1 = 2,r2 = 2,r3 = 4). S=40 * 2 + 45 * 2 + 36 * 4 = 314
    314 : 60 = 5 a zbytek je 14.
  7. Počet letadel určíme ze seskupení na obr.
    obr3
  8. Hráč K sice prohrál podle dohody s L a M, ale vyhrál nad N. Hráč N prohrál s K, ale vyhrál nad M. Hráč L vyhrál nad M. Proto hru zaplatí M.
  9. Číslo, které jste napsali na papírek, označíme písmenem x, druhé číslo písmenem y. Po prvním výkonu dostaneme y + 99 - x. Protože x není větší než 50 a y leží mezi 51 a 99 není číslo y + 99 - x menší než 100, ale není ani větší než 199. Je to tudíž vždy trojmístné číslo a jeho první číslice je 1. Přeškrtnutím jedničky se také číslo zmenší o 100; proto druhý výkon vede k číslu y + 99 - x - 100 + 1 = y - x. Poslední výkon y - (y - x)=x dává výsledek x.
  10. Označme počet zápalek, které si vzal první účastník, číslem 4k, počet druhého je potom 7k a třetího 13k. Po první změně bude mít první 8k, druhý 14k a třetí 4k. Po druhé změně bude mít první 16k, druhý 4k a třetí 4k. Po třetí změně budde mít první 8k , druhý 8k i třetí 8k. První účastník měl na začátku polovinu tohoto množství. Dělením tohoto množství čtyřmi a násobením sedmi dostaneme, kolik měl na začátku druhý účastník a dělením tohoto množství sedmi a násobením třinácti dostaneme, kolik měl na začátku třetí účastník.
  11. Vyměníme 6 a 7, dále 10 a 11.
  12. Bylo třeba vzít čtyři boty a tři ponožky. I když vezme mezi prvními třemi botami každou z jiného páru, bude čtvrtá bota určitě tvořit pár s nějakou již vybranou botou. Jestliže ponožky byly jen ze dvou druhů, bylo třeba vzít jen tři ponošky.
  13. Je 24 možností rozdělení poukazů. Označme rekreanty písmeny X, Y, Z, R a poukazy písmeny A, B, C, D. Jednotlivé možnosti rozdělení poukazů jsou ve sloupcích.
    X A A A A A A B B B B B B C C C C C C D D D D D D
    Y B B C C D D A A C C D D A A B B D D A A B B C C
    Z C D B D B C C D A D A C B D A D A B B C A C A B
    R D C D B C B D C D A C A D B D A B A C B C A B A
  14. První den v týdnu může být buď jasno nebo zamračeno. V průběhu dvou dní se mouhou jasné a zamračené dny střídat takto:
    1. možnost: první den jasno ,druhý den zamračeno,
    2. možnost: první den jasno ,druhý den jasno,
    3. možnost: první den zamračeno ,druhý den jasno,
    2. možnost: první den zamračeno ,druhý den zamračeno.
    K vystřídání všech těchto možností by byly třeba 4 dny. Při třech dnech se spojuje každá ze čtyř kombinací prvních dvou dní se dvěma možnosti třetího dne, čímž vzniká 8 možností. V průběhu čtyř dní to bude 8 * 2 atd. Za sedm dní to bude 27 = 128 rozličných možností. Jestliže k realizaci jedné této možnosti potřebujeme týden k realizaci všech 128 možností potřebujeme 128 týdnů.
  15. Váha datlí, tržby prodavačů a útraty za víno jsou v poměru 1:2:3. I utržil 48 peněz, Baltazar dostal od svého prodadvače po odečtení jeho útraty 69 peněz. Tyto dva obnosy jsou v poměru 48:69, tj. přibližně 2:3, čili Baltazarův prodavač utržil 48 * 3/2 = 72 peněz, tudíž utratil 3 peníze. Protože P utratil jeden peníz, platil třetí prodavač 2 peníze, za libru datlí utržili 1+2+3=6 peněz. I měl 48:6=8 liber, jeho pán je Melichar. Protože prodavač Baltazara zaplatil 3 peníze, nemhl to být P, byl to R a P byl prodavačem pana Kašpara.
  16. Besedy se zůčastnili 4 studenti. Každý zástupce vysoké školy získal jednoho studenta. Jeden student se nepřihlásil na žádný obor.
  17. Navrhl zalít kuličky v poháru vodou tak, aby všechny byly úplně ponořené. Objem nalité vody a ponořených kuliček bylo možno zjistit na stupnici kalibrované nádoby. Jestliže naměřený objem nalité vody odečteme od celkového objemu, dostaneme objem všech použitých kuliček. 
  18.      
	 MERRY XMAS TO ALL
	 34225 7396 81 900
	 27556 3249 81 400
  19. 1/2 * 15 * 15 * 15 = 1700g = 1,7kg.
  20. Obdelníky složené ze dvou čtvrců jsou: mn, ij, ef, ab, no, jk, fg, bc, op, kl, gh, cd, mi, nj, ok, pl, ie, jf, kg, lh, ea, fb, gc, hd, dohromady 24.
    Obdelníky složené ze čtyř čtveců jsou: mnop, ijkl, efgh, abcd, miea, njfb okgc, plhd, dohromady 8.
    Obdelníky složené ze šesti čtveců jsou: mnoijk, ijkefg, efgabc, nopjkl, jklfgh, mienjf, njfokg, okgplh, ieajfb, jfbkgc, kgclhd, dohromady 12.
    Obdelníky složené z osmi čtveců jsou: mnopijkl, ijklefgh, mieanjfb, njfbokgc, okgcplhd, dohromady 6.
    Obdelníky složené z dvanácti různých čtveců jsou: mnopijklefgh, ijklefghabcd, mieanjfbokgc, njfbokgcplhd, dohromady 4.
    Celkem je možno vytvořit 70 různých obdelníků.
  21. Zjistíte ciferný součet výsledného rozdílu (7+2+8=17). Odečteme-li tento součet od nejbližšího násobku devíti, dostaneme přeškrtnutou číslici. V tomto případě 18-17=1. Přeškrtli jsme číslici 1.
    Vysvětlení: Rozdíl mezi libovolným číslem a jeho ciferným součtem se vždy dá dělit devíti. Ciferný součet zmenšený o hodnotu vyjádřenou přeškrtnutou číslicí při dělení devíti bude mít týž zbytek jako takto vytvořené nové číslo, budeme-li je dělit devíti. Jestliženyní od nově vytvořeného čísla odečteme ciferný součet původního čísla, snížíme rozdíl o tolik jednotek, kolik vyjadřovala přeškrtutá číslice. Rozdíl se dá dělit devíti. Číslice, kterou se tento rozdíl doplní na násobek devíti, je hledanou číslicí.
  22. Při očíslování knihy se vyskytuje 9 jednociferných čísel (tj. 9 číslic), 90 dvojciferných čísel (tj. 180 číslic) a 399 trojciferných čísel (tj. 1197 číslic). Celkem se tudíž použilo 9+180+1197=1386 číslic.
    Číslice 0 se při zápisu jednociferných čísel nevyskytuje. Při zápisu dvojciferných čísel je potřebná v 9 případech. Z trojciferných čísel vezmeme nejdříve čísla menší než 110 (11 nul), dále větší než 109 a menší než 200 (dalších 9 nul). K zapsání všech trojciferných čísel menších než 500 je třeba 4*(11+9)=80 nul.
    Hledaný počet nul je 9+80=89.
  23. Rozdíl mezi dělitelem a zbytkem je v každém z uvedených případů 2. Nejmenší společný násobek čísel 3, 4, 5 a 6 je 3 * 4 * 5 = 60. Odečteme-li 2, dostaneme 58, což je hledané číslo. Takových čísel je nekonečně mnoho, další je 2 * 60 - 2 = 118, 3 * 60 - 2 = 178 std.
  24. Vepište jedno písmeno na kterékoli pole úhlopříčky AC, např. do levého horního rohu (viz. obr.). Jedno pole druhé úhlopříčky BD léží v témže řádku jako první písmeno. Druhé pole leží v témže sloupci jako toto písmeno. Do těchto dvou polí už nemůžeme vepsat další písmena. Můžeme však vepsat další písmena na jedno ze dvou dalších polí úhlopříčky BD. Poloha dalších dvou písmen je tím již určená, neboť v obou neobsazených řádcích je jen po jednom poli, kam je možno podle odmínek úlohy uložit další dvě písmena.
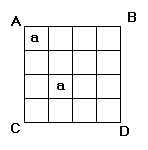
    není těžké vypočítat, kolik může mít úloha řešení. Pro každou ze čtyř možných poloh prvního písmene na jednom poli úhlopříčky AC jsou dvě možnosti umístění druhého písmena na úhlopříčce BD. Dohromady je 4*2=8 možností.
    obr4
  25. Úloha má mnoho řešení. Např.:
    (5 + 7)-(5 - 7) = 14, obráceně 41
    (13 + 17) - (13 - 17) = 34, obráceně 43 std.
  26. Karel dal Ferdovi 4 žemle a Jožka 1 žemli. 15 Kč si proto rozdělili tak, že Karel dostane 12 Kč a Jožka 3 Kč.
    (15 Kč : 5 = 3 Kč); 4 * 3 Kč = 12 Kč; 1* 3 Kč = 3 Kč

Úkoly
* Kurzy * Akcie * Práce * Zájezdy * Zájezdy * Meteobox * Auto *